Question 42 Tale

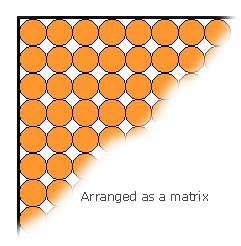
As the Hansom pulled up at the Baker Street address, Holmes and I alighted and made a quick dash for the shelter of the portico. It was in the latter days of September, and the equinoctial gales had set in with exceptional violence. All day the wind had screamed and the rain had beaten against the windows, so that even here in the heart of great, hand-made London we were forced to raise our minds for the instant from the routine of life, and to recognize the presence of those great elemental forces which shriek at mankind through the bars of his civilization, like untamed beasts in a cage. Given our damp disposition, I might have expected the great detective to be at least a little bit grumpy.

We were still lodging together (for I was not yet married), and so I had learned to read his moods and to be able to predict them with some accuracy. But even so, he seemed more than usually out of sorts. His customary sanguine countenance had clearly been ruffled by the experiences of that evening's meeting.

We had just returned from a boink arranged by the local chapter of the Numismatist's Society. Normally these were affable occasions where members might quaff an ale in good fellowship. A cosmopolitan band would arrange to meet every so often at a local watering hole. That evening it had been at the Pomfret Castle, within easy walking range just down the road. "Barely sufficient time to mentally conduct the overture to Tchaikovsky's Capriccio Italien" Holmes had grumbled to me as we walked there. Its location made it hardly worth the bother of hailing a cab for the journey home. But this evening had been different. Holmes had insisted on taking a Hansom back. Clearly the events of the evening had triggered some kind of reaction in him. He had fallen into conversation with a man who lived close by in Marylebone, and who claimed to occupy a position of some importance at a bank whose very headquarters were situated on our own Baker Street. The conversation had been friendly, but I had sensed that Holmes was paying closer than normal attention while apparently engaged in harmless banter with the gentleman.

After we were upstairs again and ensconced comfortably in front of the fire in our dressing gowns, Holmes pulled out his pipe and began to fill it thoughtfully. I knew from his demeanor something was afoot, so I ventured to ask about his conversation at the boink.

"The man is not what he would have us believe he is" said Holmes. I raised my eyebrows and awaited further elucidation.

"He claims to be an expatriate American working here in a bank, but that doesn't wash with me." After striking a Vesta on the sole of his slipper, Holmes continued. "He says his name is Garry spelled with two R's. That is clearly not the mark of an American pretending to be an Englishman. Rather I fear it is an Englishman pretending to be an American pretending to be an Englishman."

"Great Scott Holmes!" I remonstrated. "Hardly sufficient evidence to question the man's ancestry, and besides, how in the name of Hades do you draw that conclusion?"

"It's quite simple" he murmured as he gave a thoughtful pull on his pipe, and puffed a cloud of fine Turkish Latakia into the fireplace draught. "Gary with a single R is of course a quintessentially American name, but an Englishman would never allow himself to be identified by such a handle—as our supposedly Yankee friend might put it—lest he be mistaken for some crude wheeled conveyance from the Indian sub-continent."

I knew from my time with the Khyber Rifles that the Bengali word ghari (which is pronounced by the natives with the sound /a/ as represented in ASCII IPA, but pronounced by British officers as /&/) is their term for almost any form of cart or wheeled transportation. But I failed to see what my friend was driving at.

Holmes continued "Only an Englishman would take such pains to ensure that his name was not a homophone for a Bengali native jitney. An American would not even be aware of the problem. But the Englishman would insist on using the double R, thus ensuring that it rhymes with 'carry' and not with 'sari'".

"And on that you base your conclusion that he isn't what he says he is?" I asked.

"No—there is more" said Holmes. "To test his posture as banker and numismatist, I asked him the Moriarty question, and he failed miserably. No man who claims to be a banker boinker in good standing would fall into such an elementary trap."

I raised one eyebrow and urged my friend to continue.

"The question is posed as to how many undamaged American pennies can be made to fit within the confines of a cube with 1-foot sides. A poseur might go to the Web and after examining the page at http://www.kokogiak.com/megapenny/four.asp give the answer that is shown there as 49,152. Or a man of agile arithmetic abilities might work it out for himself. As each penny is ¾ inch in diameter, it is clear that one can fit a row of 16 in one direction and 16 in the other direction, to give a length times breadth of 16 multiplied by 16 which gives 256 pennies per layer. Then it is but a simple matter to calculate how many layers at 1/16th of an inch will go to make up the vertical foot, multiply by 256 and you get what you might think is the correct answer—but you would be wrong!"

My look of puzzlement evidently goaded him on.

Holmes reached for the paper doily covering the jug of water that he used to dilute his whiskey when drinking before midday. He pulled a finely crafted Parker from his dressing-gown pocket and drew a diagram on the back of the doily which I reproduce in part below.

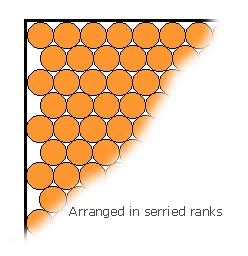
"Now observe" said Holmes, "that there is a fundamental problem here. As any fule kno, above a certain minimal area, optimal packing for circles within a rectangle is achieved in a hexagonal array. The 'height' of an N-row hexagonal array of circles with diameter d is H = d + (N-1)sqrt(3)d/2."

Holmes then went on to explain this to me in further detail. Here is an extract from the notes that I made at the time:

N = int[(2H - 2d) / sqrt(3)d] + 1 for the number that fit into a given array height. (Where int is the greatest-integer or 'floor' function.) For a height of 12 inches and a diameter of 3/4 inch, this gives 18 rows. Thus, assuming a 1-foot square laid out on the floor and oriented to the compass points, we start the first row of pennies along the southern boundary, and this has 16 pennies in it which makes exactly 1 foot. In the next row, we use only 15 pennies, but shifted sideways by a half-diameter and snugged into the first row. And we can have 18 of these rows as I calculate thus: 1) In this arrangement, the first row takes d, each subsequent row takes d*sqrt(3)/2 2) n rows therefore take d + (n-1)*d*sqrt(3)/2 3) To fit n rows in 16d, 16d = d + (n-1)*d*sqrt(3)/2 which simplifies to n = 1 + 10*sqrt(3) n = 18.3205 Then considering the 'pairs of rows' each containing a total of 16 + 15 pennies, we can fit 9 of these row-pairs within the north-south dimension (with a little bit left over), giving a total for this first layer of 9 * (16 + 15) = 279 pennies, which clearly is more than the 256 one would find if the pennies were arranged as a simple matrix.

Holmes turned to the other side of the paper doily and drew another diagram to show this arrangement, which I reproduce in part below.

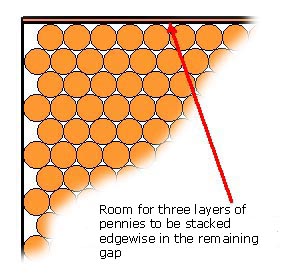
"Aha!" I cried. "So we have to multiply the number of layers times 279 instead of 256?"

"No—not so fast" said Holmes.

"Remember, these 18 rows stretching in the North/South dimension don't actually take up the whole 1-foot—there is a little bit left over, and into this gap, we can tuck in some number of vertical layers. Remember too that a vertical wall is also 1-foot square, so each of these vertical layers that we are going to tuck in will also consist of 279 pennies."

"Aha!" I cried. "The left-over gap was 0.3205 of the diameter of a penny, over and above the 18 we calculated above, so we can add three layers of 279 pennies each."

Holmes had meanwhile modified his diagram to show the extra three layers.

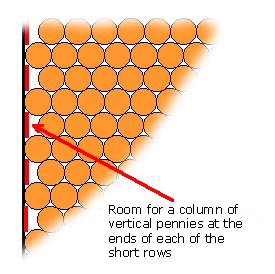
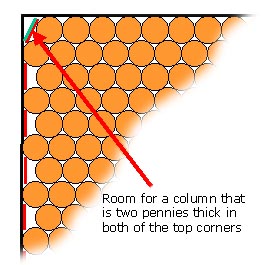
"So there you have the answer!" I said, but with a sinking feeling as I saw his countenance darken.

"No—not so fast" said Holmes, "There is a little more to it than that." He searched around for another piece of paper on which he could scribble. Eventually he retrieved an advertising booklet for the new Bakerloo commuter service to Mornington Crescent, and started drawing on the rear cover which was blank.

"Observe, that in taking this strategy of optimal packing of circles within a rectangle, that we now have nine short rows with a little space at each end, and in that space maybe we can fit a column of pennies edgewise." He showed me his latest diagram.

"The question is now what thickness of pennies each of these columns might be able to contain. It turns out that the answer is just a hair under two." The notes I took at the time read as follows:

The centres of the pennies on rows 1 and 3 are separated by d*sqrt(3). A column of width d, edge-on to the ends of rows 1 and 3 and centred on row 2, intersects the end pennies at height h, calculated thus: The triangle at the centre of a penny and the point of intersection gives (d/2 - h)**2 + ((d*sqrt(3)-d)/2)**2 = (d/2)**2 (d-2h)**2 + (d*0.732)**2 = d**2 Write s=h/d (1-2s)**2 + 0.536 = 1 (1-2s)**2 = 0.464 1-2s = 0.681 s = 0.159 h = 0.159d = 0.120in = 1.92 penny-thicknesses Thus we conclude that there is room for a column that is one penny thick. And of course each column is 16 pennies high to fit in the 1-foot height of the cube."

(I later double-checked Holmes' calculations using some of the surveying instruments which I brought back after the Uttar Pradesh mapping expedition. The document was later filed with my other important papers in The Bodleian. My readers who are more visually adept than mathematically inclined, may consult it there.)

"Aha!" I ejaculated. "So we have 18 columns of pennies (9 on each side of the cube), so we have to add 18 times 16 pennies to the total. Very clever, Holmes! You've done it again!"

"No—not so fast" said Holmes. He looked slightly pained that I had once more come prematurely to a conclusion .

"What you failed to observe" he continued, "is that the space for the short row of pennies at the very end of the cube is larger than the other spaces because it is not constrained by the curvatures imposed by yet another serried row of pennies beyond it. Because the column of pennies in this last gap can be angled slightly sideways, this column can in fact be made two pennies thick instead of just one thickness." Holmes leafed through the advertising booklet for the Mornington Crescent service looking for a white space in which he could draw another diagram. After licking the nib of his Parker to ensure ink flow, he drew the following:

"Aha!" I ejaculated for the second time. "Surely now we are at the climax of the problem."

Holmes tapped out the dottle from his pipe on the back of his slipper. "Yes indeed, my friend, at least we have the answer to this mathematical portion of the conundrum. It may be conveniently summarized thus—" and he proceeded to write out the following bill on the back of the receipt from the Hansom cab in which we had returned that evening.

I turned to Holmes after this brilliant exposition, but there was still something nagging me. "While that may call into question the credentials of our fellow boinker as a numismatist banker, surely that gives you no cause to doubt his ancestral antecedents?"

"Aha!" said Holmes. "You failed to observe one other vital clue. When the gentleman with two R's in his name gave me his answer, the figure he arrived at was not the simple one of 192 layers each of 256 pennies. No—from the number he supplied, I deduced that he thought there were 196 layers of pennies to the foot instead of just 192. That clinched it for me that he was not an American as he claimed, but he must be an Englishman posing as an American posing as an Englishman."

I must have looked perplexed, because Holmes now tapped his pipe in an irritated manner against his right temple. "This means he was working with the thickness of pennies expressed as 1.55 millimetres, which is of course a classic case of approximation by metrication. Yet another unfortunate example of what the government in Westminster has inflicted upon us. A true American who knew that the diameter of a penny was defined as 3/4 of an inch, would never then go on to think of its thickness in terms of millimetres, when it was obviously designed in a world of rational fractions of feet and inches. No—I fear only an Englishman, who has become confused and bemuddled by the imposition of metric law, would make such a fundamental mistake. And through this he exposed himself for what he is!"

Holmes put his pipe in the ash-tray and reached for his violin. Clearly there was no more to be said about the case, but I resolved to document it in some detail, in case investigators in years to come might benefit from Holmes' methodology.